Aplicaciones en EconomíaEn la Economía también es importante considerar la variación de una cantidad respecto a otra. Por ejemplo la demanda de un producto respecto a su precio, o el precio de un producto respecto a su costo de producción o la utilidad obtenida en la venta de un producto, con relación al costo de producción, etc.
Por lo anterior, es muy importante la representación de las cantidades relacionadas en forma de funciones que puedan ser derivables, no obstante que los datos que se manejan sean discretos, por ejemplo cuando se establece la función de costo 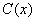 , la variable x representa unidades de cierta mercancía.
, la variable x representa unidades de cierta mercancía.
ObjetivoResolver algunos problemas sencillos en Economía.
Conceptos previos
En Economía se suele describir la variación de una cantidad respecto a otra mediante un concepto llamado promedio que expresa la variación de una cantidad sobre un rango específico de valores de otra y un concepto llamado marginal que expresa el cambio instantáneo en una cantidad respecto a la otra.
Un símil de los conceptos anteriores en Física serían los conceptos de velocidad promedio y velocidad instantánea o lo que geométricamente serían la pendiente de la recta secante y la pendiente de la recta tangente, respectivamente.En Economía se suele describir la variación de una cantidad respecto a otra mediante un concepto llamado promedio que expresa la variación de una cantidad sobre un rango específico de valores de otra y un concepto llamado marginal que expresa el cambio instantáneo en una cantidad respecto a la otra.
- Un ejemplo:
- Si
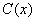 es la función que representa el Costo Total en unidades monetarias para producir x unidades de cierta mercancía:
es la función que representa el Costo Total en unidades monetarias para producir x unidades de cierta mercancía: - El costo promedio de producción de cada unidad, sería el costo total entre la cantidad de unidades de mercancía producidas, es decir:
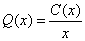 , a la cual se le llama función del Costo Promedio.
, a la cual se le llama función del Costo Promedio. - El costo marginal cuando
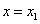 es
es 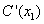 , si esta cantidad existe. Y se interpreta como la razón de cambio instantánea del Costo Total con respecto al cambio unitario en las unidades producidas, cuando se producen
, si esta cantidad existe. Y se interpreta como la razón de cambio instantánea del Costo Total con respecto al cambio unitario en las unidades producidas, cuando se producen 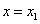 unidades.
unidades. - De manera similar
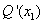 sería el Costo Promedio Marginal cuando
sería el Costo Promedio Marginal cuando 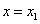 y que representa la razón de cambio instantánea del Costo Promedio cuando
y que representa la razón de cambio instantánea del Costo Promedio cuando 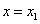 .
.
- Si
- Otro ejemplo
- Si p es el precio de unitario de cierta mercancía y x el número de unidades de dicha mercancía. Es natural pensar que la cantidad solicitada por los consumidores en el mercado, dependa de su precio. Es natural pensar que "a menor precio, mayor demanda y a mayor precio, menor demanda".
- A veces también es posible considerar que el precio de un producto se puede establecer en función de su demanda: "a mayor demanda menor precio". En este caso, tendríamos p = g(x) que se llamaría función de demanda o inclusive podría establecerse mediante una ecuación de demanda. A la gráfica correspondiente que relaciona cantidad x solicitada y el precio p, los economistas acostumbran llamarle curva de la demanda.
Aquí un caso típico de curva de demanda- Un caso típico: La demanda de un cierto producto es nula cuando el precio es muy alto (p=18), mientras que el consumo máximo de dicho producto en una familia no puede pasar de cierto valor (6 unidades) aun que el precio fuese cero.
- Derivado de estos conceptos, se tiene la función de Ingreso Total, R(x) = x P(x), es decir: la cantidad de unidades vendidadas, por el precio de las mismas.
- Y además la función de Ingreso Marginal, R'(x) = P(x) + x P'(x), que representaría la razón de cambio del ingreso total para cada x.
Da clic en un ejemplo, ejecútalo y da clic en el icono de reiniciar 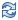
EjerciciosEn los ejercicios siguientes, se plantea un problema sobre la producción de ciertas mercancias, conociendo la función del Costo Total y donde se desea conocer la razón de cambio en los costos de producción, para valorar la conveniencia de la inversión. Recuerda que debes tomar lápiz y papel para intentar resolverlo.
http://www.objetos.unam.mx/matematicas/matema/Daplica/da_aplicacion05_d.html
http://www.objetos.unam.mx/matematicas/matema/Daplica/da_aplicacion05_d.html
No hay comentarios:
Publicar un comentario